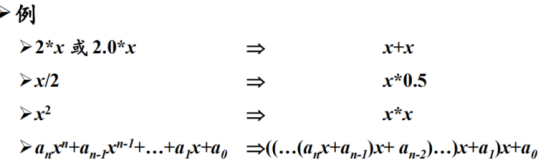天辰注册

CURRICULUM

天辰APP下载

0898-08980898

广东省清远市

123456789

天辰新闻 >更多

天辰新闻

当前位置：首页 > 天辰新闻

编译原理（8）：代码优化

2024/06/24

声明：本系列文章，是根据中国大学MOOC网哈工大的编译原理这门课学习而成的学习笔记。

基本块(Basic Block)

基本块是满足下列条件的最大的连续三地址指令序列

控制流只能从基本块的第一个指令进入该块。也就是说，没有跳转到基本块中间或末尾指令的转移指令
除了基本块的最后一个指令，控制流在离开基本块之前不会跳转或者停机

基本块划分算法

在这里插入图片描述

首先（1）指令是首指令，其次跟在跳转指令的目标指令（5）（9）（23）是首指令，最后紧跟跟在跳转指令之后的指令（9）（13）（14）（23）是首指令。

流图(Flow Graphs)

流图的结点是一些基本块
从基本块B到基本块C之间有一条边当且仅当基本块C的第一个指令可能紧跟在B的最后一条指令之后执行
此时称B是C的前驱(predecessor) ，C是B的后继(successor)
有两种方式可以确认这样的边：
1. 有一个从B的结尾跳转到C的开头的条件或无条件跳转语句
2. 按照原来的三地址语句序列中的顺序，C紧跟在之B后，且B的结尾不存在无条件跳转语句

图中，B6不是B5的后继，因为B5的结尾存在一个无条件跳转指令

优化的分类

机器无关优化：针对中间代码
机器相关优化：针对目标代码
局部代码优化：单个基本块范围内的优化
全局代码优化：面向多项基本块的优化

常用的优化方法

删除公共子表达式
删除无用代码
常量合并
代码移动
强度削弱
删除归纳变量

① 删除公共子表达式

公共子表达式
如果表达式x op y先前已被计算过，并且从先前的计算到现在，x op y中变量的值没有改变，那么x op y的这次出现就称为公共子表达式

B5中的t7和t6重复，t8和T10重复，构成局部公共子表达式，可以删除t7，t10，并将对t7和t10的引用换成t6和t8，如右上角所示。

B5中的t6和B2中的t2一样，并且，从B2到B5的过程中i的值没有改变，故t6和t2构成全局公共子表达式，可以用t2代替t6，同理t4可以代替t8

替换后，发现再次构成公共子表达式，可以继续替换

② 删除无用代码

复制传播

常用的公共子表达式消除算法和其它一些优化算法会引入一些复制语句(形如x = y的赋值语句)
复制传播：在复制语句x = y之后尽可能地用y代替x
复制传播给删除无用代码带来机会
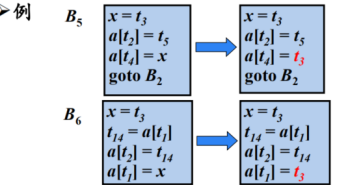
无用代码(死代码Dead-Code ) ：其计算结果永远不会被使用的语句

③ 常量合并(Constant Folding)

如果在编译时刻推导出一个表达式的值是常量，就可以使用该常量来替代这个表达式。该技术被称为常量合并
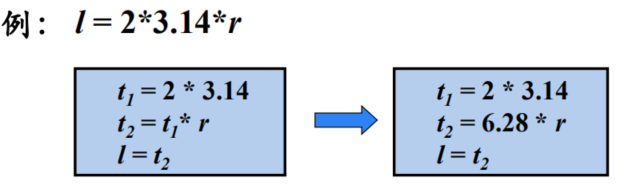
在这里插入图片描述

④ 代码移动(Code Motion)

这个转换处理的是那些不管循环执行多少次都得到相同结果的表达式(即循环不变计算，loop-invariant computation) ，在进入循环之前就对它们求值
在这里插入图片描述
循环不变计算的相对性：对于多重嵌套的循环，循环不变计算是相对于某个循环而言的。可能对于更加外层的循环，它就不是循环不变计算

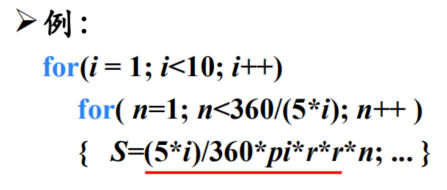
⑤ 强度削弱(Strength Reduction)

用较快的操作代替较慢的操作，如用加代替乘
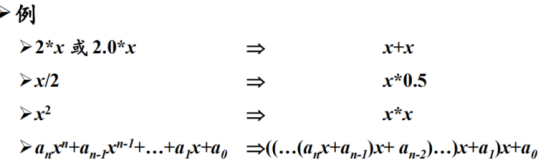
在这里插入图片描述

循环中的强度削弱

归纳变量：对于一个变量x ，如果存在一个正的或负的常数c使得每次x被赋值时它的值总增加c ，那么x就称为归纳变量(Induction Variable)

⑥ 删除归纳变量

在沿着循环运行时，如果有一组归纳变量的值的变化保持步调一致，常常可以将这组变量删除为只剩一个
在这里插入图片描述

很多重要的局部优化技术首先把一个基本块转换成为一个无环有向图(directed acyclic graph，DAG)

基本块的 DAG 表示

在这里插入图片描述

基于基本块的 DAG 删除无用代码

e删除后，b和c就根节点。

数组元素赋值指令的表示

在这里插入图片描述

根据基本块的DAG可以获得一些非常有用的信息

在这里插入图片描述

从 DAG 到基本块的重组

在这里插入图片描述

首先L是活跃变量，故保留L，删除M；其次判断根节点，G不是活跃变量，故可以删除，其次，有两个名字的保留一个名字，最后直接使用常量，删除B和K

数据流分析(data-flow analysis)

数据流分析
一组用来获取程序执行路径上的数据流信息的技术
数据流分析应用
到达-定值分析 (Reaching-Definition Analysis)
活跃变量分析 (Live-Variable Analysis)
可用表达式分析 (Available-Expression Analysis)
在每一种数据流分析应用中，都会把每个程序点和一个数据流值关联起来

数据流分析模式

在这里插入图片描述

基本块上的数据流模式

在这里插入图片描述

到达定值分析

在这里插入图片描述

B1中d1，d2，d3到B2的入口处，没有对i，j，a进行重新赋值，故这三个定值都可以到底B2的入口处；从d4之后的路径到底B2入口处，必然会经过d7对i的重新赋值，d7杀死了d4，故d4不能到达B2入口处，其他类似。其中，注意d3可以到达B4的入口处，可以不经过B3，所以，注意可能这个说法

到达定值分析的主要用途

循环不变计算的检测
如果循环中含有赋值x=y+z ，而y和z所有可能的定值都在循环外面(包括y或z是常数的特殊情况) ，那么y+z就是循环不变计算
常量合并
如果对变量x的某次使用只有一个定值可以到达，并且该定值把一个常量赋给x ，那么可以简单地把x替换为该常量
判定变量x在p点上是否未经定值就被引用

“生成”与“杀死”定值

在这里插入图片描述

到达定值的传递函数

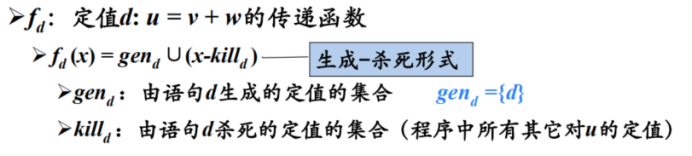
在这里插入图片描述

到达定值的数据流方程

在这里插入图片描述

到达定值方程的计算

计算到达定值的迭代算法
在这里插入图片描述

引用-定值链 (Use-Definition Chains)

在这里插入图片描述

活跃变量分析

活跃变量
对于变量x和程序点p，如果在流图中沿着从p开始的某条路径会引用变量x在p点的值，则称变量x在点p是活跃(live)的，否则称变量x在点p不活跃(dead)

在所有的块中，都没有对a的应用，故a是不活跃的。
i在B1后，必然会经过B2，B2中对i进行了引用，故i在B1出口处是活跃的，经过B2后，必然经B4对i进行重新赋值，故i在B2和b3的出口处不是活跃的，但在B4后，i可能会经过B2对其引用，故i在B4出口是活跃的。
控制重任意一个块离开后，都会进入B2，故，j在任何出口处都是活跃的，其他的类似。